CEOI2017·Mousetrap

题解

树上博弈是真的好玩……

首先看到这道题发现答案具有单调性，于是想到可能会二分。

先钦定陷阱所在的结点为根节点，这样老鼠向陷阱走的过程就是向根节点走的过程

先考虑这样一种情况：

Bob 刚开始只在当前子树中向下走

通过画图模拟可以发现，当 Bob 向下走走到叶子节点或其通往更深层的子树的边都被 Alice 封住的时候，它就陷入了一个通往父亲结点的路被弄脏，向下又走不通的局面，这时 Alice 不要先去清理路径让 Bob 向上走，而是要去做另一些有意义的事情

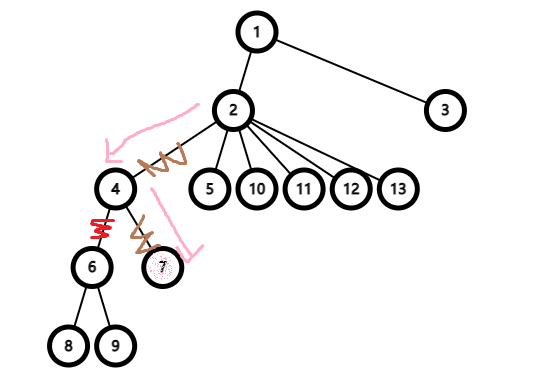
如上图，假设（注意只是假设，不要去问为什么 Alice 刚开始不去堵 $2\to 4$ 的边） Bob 初始在二号结点，最后被堵在了七号节点，棕色的边是被弄脏了的边，红色的是被堵住的边。现在 Alice 该做什么呢？

显然不是去清理路径直接放 Bob 向上走，因为 Bob 向上走的时候可能会遇到其他可以进入的子树再跳下去，不会让减少 Alice 的操作次数。所以 Alice 要趁 Bob 不能走的时候，将其之后向上走的路径上通往其他子树的边全部堵住。

接下来来探究 Bob 的策略：

设 $dp_u$ 为以 $u$ 为根的子树中， Bob 在 $u$ 处出发，双方均使用最优策略，且 Alice 使得 Bob 最后回到 $u$ 处，Alice 的最少操作数

如果 Bob 在 $x$ 处且他已经知道了所有 $y\in son(x)$ 的 $dp$ 值，显然，他会往最大的那个 $dp_v$ 的子树走，然而 Alice 希望花费数尽可能的少，所以他会堵住通向 $dp$ 值最大的那棵子树的边，于是状态转移方程呼之欲出：

$$dp_u=|son(u)|+2\text{nd}\max_{v\in son(u)}dp_v$$

其中，$\text{2nd}\max$ 是次大值

但是，Bob不一定刚开始只在当前子树中向下走，也有可能向上走

考虑二分

求出 $g_x$ 表示根节点到 $x$ 的路径中所有分叉路数量。

$$g_x=\begin{cases} 0,&x=t\\ g_{fa}+|son(u)|-1,&x=m\\ g_{fa}+|son(u)|-2,&otherwise\\ \end{cases}$$

设 $t\to m$ 的路径上结点集合为 $S$

对于路径上每一个点 $u$ 的分叉子树结点考虑，如果其满足以下条件，则需要堵住通往这条分叉子树的边：

$$u\in S,v\in son(u),v\not \in S\\ g[u]+dp[v]>mid$$

当前 $mid$ 不合法的条件：

• $mid$ 次操作次数不够用
• $Alice$ 的手速不如 $Bob$ ，即当 $Bob$ 走到 $u$ 处时，但 $u$ 处需要被堵住的通往分叉子树的边没有被堵住